ROMBO
CALCULAR EL ÁREA DEL ROMBO:
RESULTADO:
Calcular área del rombo es realmente muy sencillo, te ayudaremos a que termines de comprenderla. En este artículo encontraras todos los ejemplos y definiciones para sacar un sobresaliente en tu examen.
Definición de un polígono regular
Un rombo es un polígono con cuatro lados (cuadrilátero) los cuatro lados son completamente iguales. Es importante destacar que tienen cuatro ángulos interiores iguales de dos a dos.
Elementos de un rombo
Las propiedades de un rombo son las siguientes:
- Lados: el rombo tiene cuatro lados (a) idénticos.
- Ángulos: el rombo tiene cuatro ángulos (dos a y dos B) iguales de dos a dos. Los ángulos interiores, como todos los cuadriláteros, suman 360° (2π radianes).
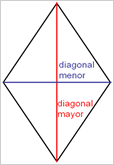
- Diagonales: los diagonales en el rombo son segmentos que van a unir los vértices no consecutivos. Estos tienen dos diagonales (D y d) desiguales y rectos. Ellos se cortan en el centro del rombo. También podríamos decir que las diagonales son las bisectrices de los ángulos que igual son ejes de simetría.
- Eje de simetría: son líneas imaginarias que van a dividir el rombo en dos partes iguales respecto a su eje. El mismo tiene dos ejes de simetría (E1 E2) que coinciden con las diagonales.
- Es importante que sepas que un caso particular del rombo es el cuadrado, ya que, todos los ángulos son iguales, es decir, (a=B). Los ángulos serán todos paralelos (de 90°) y las diagonales iguales.
Perímetro de un rombo
El perímetro de un rombo se puede encontrar por sus lados o en su defecto por sus diagonales.
El perímetro es cuatro veces la longitud de uno de sus lados (a), puesto que, tiene los cuatro lados iguales. La fórmula es la siguiente:
Perímetro = 4 . a (a es un lado del rombo)
De igual manera se puede calcular su perímetro si sabemos las diagonales del rombo que son D y d. Para ello se forman cuatro triángulos rectángulos simétricos en los que sus catetos son la mitad de las diagonales (D/2 Y d/2). El lado a será la hipotenusa y la podremos aplicar, por ende, en el teorema de Pitágoras:
a²= (D/2) ² + (d/2)² = D² + d²/4
a= /D² + d²/2
Perímetro= 4ª= a /D² + d²
Formula del rombo
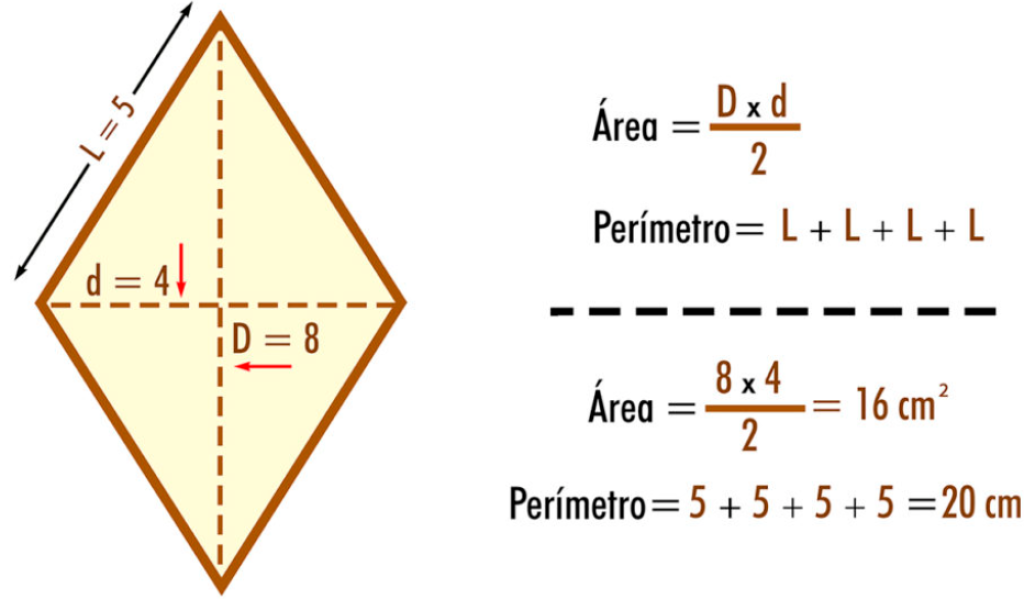
La fórmula del rombo son varias, pero la más común es mediante las dos diagonales del rombo (las D de un rombo son rectas). El área será la mitad del producto de las D y d:
Área= D.d/2 (D y d son las diagonales del rombo)
Otra forma de poder calcular el área del rombo es a través de la fórmula del área del paralelogramo. Entonces en este caso un lado se considera la base del rombo. Se mide la altura y el resultado será la base por la altura.
Área= a . h (a es la base y h la altura relativa)
Área del rombo ejemplos
Te mostraremos un ejercicio:
Un rombo que se conoce la longitud de sus D y d (la diagonal mayor D=5cm y la diagonal menor d=3 cm.
Área= D . d/2= 5 . 3/2= 15/2= 7,5cm².





