CUADRADO
CALCULAR EL ÁREA DEL CUADRADO:
RESULTADO:
¿Quieres aprender a calcular área del cuadrado? Estas en el lugar indicado, nosotros daremos una explicación sencilla y optima para la resolución de tus exámenes.
Definición de un cuadrado
El cuadrado básicamente es un polígono con cuatro lados iguales, es decir, un cuadrilátero. Es importante destacar que sus cuatro ángulos interiores son iguales y rectos, específicamente de 90° cada uno.
Se podría decir que el cuadrado es un caso particular del rectángulo, como también es un caso particular del rombo ya que sus lados y ángulos son iguales (de 90°).
Elementos de un cuadrado
Los elementos del cuadrado son los siguientes:
Lados: el cuadrado como lo mencionamos anteriormente tiene cuatro lados (a) iguales y rectos.
Ángulos: el cuadrado tiene cuatro ángulos (a) iguales y paralelos de 90° (π/2 radianes).
Diagonales: las diagonales son unos segmentos que se encargan de unir los vértices opuestos. Poseen dos diagonales (D1 y D2) iguales y perpendiculares. Estas son bisectrices de los ángulos, además son ejes de simetría.
Ejes de simetría: son líneas imaginarias que se encargan de dividir el cuadrado en dos partes simétricas con respecto a su eje. Es importante destacar que poseen cuatro ejes de simetría (E1, E2, E3 y E4).
Perímetro de un cuadrado
Recordando que el cuadrado tiene los cuatro lados iguales sacar el perímetro de un cuadrado es sumamente fácil, simplemente es cuatro veces uno de sus lados. Su fórmula es la siguiente:
Perímetro= 4 . a (siendo a un lado del cuadrado).
Formula del cuadrado
El cuadrado se calcula a partir de uno de sus lados (a). Este será el producto de la base por la altura del cuadrado, puesto que, al ser ambas idénticas el área será un lado al cuadrado. La fórmula del cuadrado es la siguiente:
Área = a² (recordando que a es un lado del cuadrado)
También es importante obtener las formulas para la diagonal del cuadrado (D) que se puede calcular a partir de la longitud de los lados. La fórmula para la diagonal es:
D=/2. A (siendo a un lado del cuadrado)
Dicha fórmula se obtiene directamente de la ley del paralelogramo.
Pero también podrías obtenerlas con el teorema de Pitágoras, puesto que, los dos lados (a) consecutivos del cuadrado y de la diagonal forman un triangulo rectángulo.
Área del cuadrado ejemplos
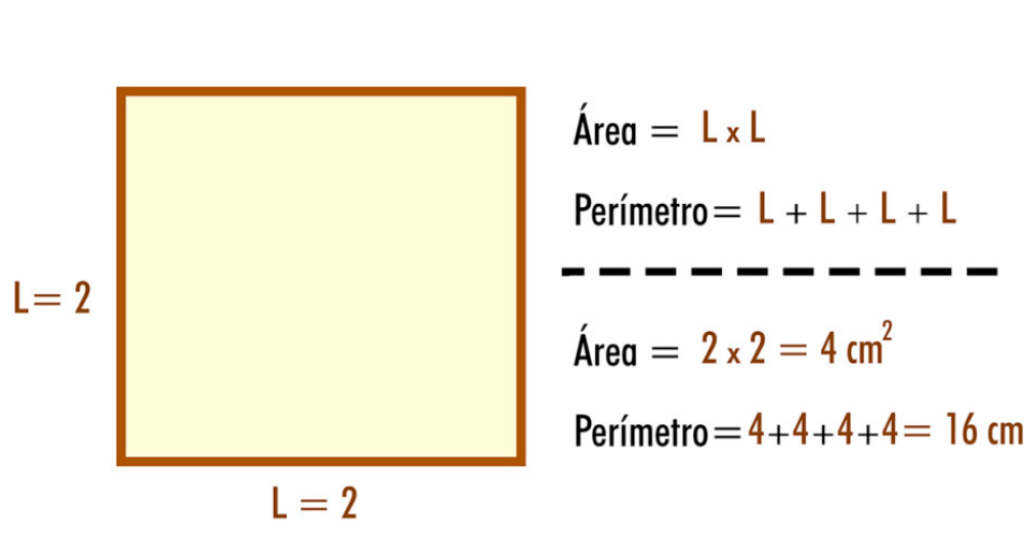
La fórmula del área del cuadrado también la podemos obtener de otra forma, directamente de la fórmula del área del paralelogramo. Específicamente solo si la base del cuadrado es uno de sus lados ya que la altura relativa a la base será un lado del cuadrado, derivando de esta manera la fórmula del área interior. Como también puede ser a partir de sus diagonales:
Área=D²/2
Área del cuadrado solución
A continuación te daremos unos ejemplos aplicables, para que tengas una idea de cómo resolver un ejercicio:
Te daremos un cuadrado cuyos cuatro lados son todos iguales, con una longitud de a=5cm.
Entonces, su área será uno de sus lados elevados al cuadrado, es decir:
Área= a²=5²=25cm²
Entonces nuestra respuesta es que el área del cuadrado de lado de 5cm es de 25cm².